Decision Tree

어떠한 input

x

에 대해 test function(

f_{m} (x)

: 분류 기준)을 계속해서 거쳐나가면서 어떠한 discrete한 값 혹은 continious한 값으로 분류하는 모델.

이 때, 분류 기준을 계속해서 거쳐나가면서 생기는 모양이 Tree 구조가 된다.

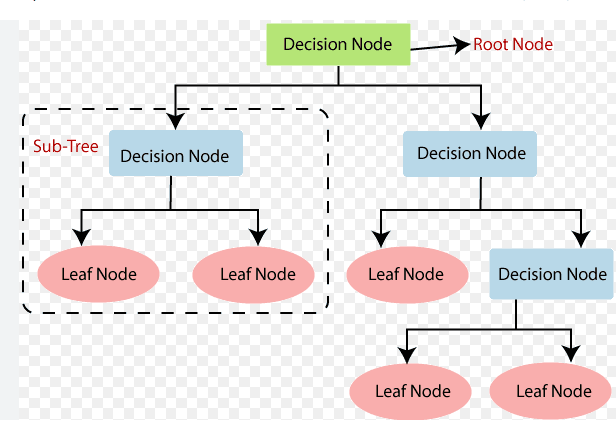
Branch: test function을 통해 나오게 되는 분기 값.
Leaf Node: output(class or numeric value(Regression))
Path: Conjuction(합성/논리곱) of branch(attribute tests: input의 특정 feature에 대한 test value)

Decision tree는, 이러한 Path들의 Disjuction(논리합)이라고 할 수 있다.
Decision tree에 input $x$ 가 들어오면, Root Node부터 시작해 재귀적으로 leaf Node에 다다를 때까지 분류되어서 하나의 Output을 가지게 된다.

Tree size

Decision Tree의 가장 큰 특징 중 하나는, Tree의 크기를 다양하게 하여 Consistent한 model을 항상 만드는 것이 가능하다는 것이다.

즉, 아무리 새로운 input이 추가되어도 Consistent한 모델을 만드는 게 가능하며, 이는 Version Space의 축소로 이어지게 되어 Overfitting으로 이어진다.

따라서, 가능하면 최대한 간단한 수준의 Tree를 model로 하는 것이 좋다.

하지만 모든 경우의 Tree의 수를 계산하는 것은 계산량이 높으므로 Entropy를 활용하여 간단한 수준의 model을 근사해낸다.
purity: 어떠한 classifier에 대하여, 가능하면 한 class는 많고 다른 class는 가능한 한 적게 분류되는 정도를 말한다. 즉, Entropy와 반비례한다. 좋은 Tree model을 만들기 위해서는 Purity가 높아야 한다.

Information Gain of Split

Purity가 높게 하기 위해서는, Information Gain이 높아져야 한다.

Information Gain(정보 공유량)은 불확실성이 얼마나 감소하는지에 대한 척도이므로, 높을수록 어떠한 attribute를 기준으로 데이터를 Split 했을 때 나눠진 그룹의 Entropy가 줄어듬을 의미한다. purity의 상승은, 더 간단한 Tree model을 만들 확률의 상승을 의미한다.

instance $x$ 가 node $m$ 에 다다를 때에 class $c_{k}$ 일 확률: $P (c_{k} ∣ x \to m) = \frac{N _{m, k}}{N _{m}} \equiv p_{m, k}$
- $N_{m, k}$ : node $m$ 속의 $c_{k}$ 에 속하는 instance들의 개수.
- $N_{m}$ : node $m$ 에 속하는 instance들의 개수.
Impurity of node $m$ (entropy): $- k \sum p_{m, k} lo g_{2} p_{m, k}$
Test function $f_{m} (x)$ 에서 $j$ 라는 branch를 따를 때 class $c_{k}$ 일 확률: $P (c_{k} ∣ f_{m} (x = j)) = \frac{N _{m \to j, k}}{N _{m \to j}} \equiv p_{m \to j, k}$
- $N_{m \to j, k}$ : node $m$ 에서 $j$ 라는 branch를 따르는 $c_{k}$ 에 속하는 instance들의 개수.
Average Impurity after split(conditional entropy): $- j \sum \frac{N _{m \to j}}{N _{m}} k \sum p_{m \to j, k} lo g_{2} p_{m \to j, k}$ : weighed sum을 이용한 평균이 된다.

이 때, Information Gain은 그 정의에 의해

- k \sum p_{m, k} lo g_{2} p_{m, k} + j \sum \frac{N _{m \to j}}{N _{m}} k \sum p_{m \to j, k} lo g_{2} p_{m \to j, k}

: node $m$ 의 impurity가, split을 통해 얼마나 제거되는 지를 나타낸 것이라 볼 수도 있다.

Tree Learning Algorithm

만약 Train Data $D$ 의 Entropy가 threshold보다 작다면 해당 $D$ 에서 가장 비중이 높은 클래스로 leaf Node를 만든다.
1. 어느 정도의 Entropy보다 작아진다면, 이는 충분히 간단한 model이라 판단하고 중지하는 것이다.
2. $D$ 는 매개변수로 재귀적으로 들어오는 형태로, 계속해서 split된 $D$ 가 threshold보다 작을 경우 종료한다.
$D$ 에 대한 적절한 test function $f_{m}$ 을 찾는다.
$f_{m}$ 의 모든 branch에 대해 $D$ 를 $f_{m}$ 을 거쳤을 때 해당 branch가 나오는 instance들 끼리 묶는다.
각각의 묶은 데이터 셋 $D_{j}$ 에 대해 위의 과정을 재귀적으로 반복하고, 그렇게 만들어진 Sub-tree를 현재 Node $m$ 의 $j$ -th child로 만든다.

위의 과정을 거치면서, Decision Tree가 만들어진다.

Find Test Function $f_{m}$

For discrete value

어떠한 Data set $D_{j}$ 의 instance $x$ 의 모든 feature에 대해서,
각각의 feature가 $v$ 개의 값으로 나누어진다면 $D_{j}$ 를 $v$ 개로 분류하고,
분류한 $v$ 개의 데이터셋들에 대한 Information Gain을 구한다.
이 때, Inforamtion이 가장 크게 되었던 feature를 택해 $v$ 개의 branch를 내놓는 $f_{m}$ 을 만든다.

for continious value

어떠한 Data set $D_{j}$ 의 instance $x$ 의 모든 feature에 대해서,
$D_{j}$ 를 어떠한 midpoint에 의해 두 개의 데이터 셋으로 나눈다.
1. 이 때, midpoint는 값이 변하는 점만을 고르다면 그 때 information gain이 커지므로 변하는 점만을 고르면 된다.
2. 값이 변하는 점을 기준으로 비슷한 값들이 모여 있을 확률이 높으니 inforamtion gain이 높아질 확률이 높다.
split된 두 개의 데이터셋에 대한 information Gain을 구해,
가장 Information Gain이 컸던 feature의 midpoint( $m$ )를 이용해 $f_{m} (x) : x_{i} < m$ 을 구한다.

Pruning

가지치기. Decision Tree에서 성능을 개선하기 위해 불필요하게 복잡한 부분을 없애 VC Dimension을 낮추는 방법이다.

VC Dimension의 상승은 Noise나 특수한 패턴에 민감하게 반응하게 되어 Overfitting으로 이어진다.

Prepruning: Tree를 완전히 성장시키지 않고, 성장을 제한하는 방법. 만약 특정 조건을 만족하면 분기하지 않고 해당 Node를 Leaf Node로 처리한다. 계산 속도가 빠르다는 장점이 있다.
Postpruning: Tree를 완전히 성장시킨 후, 성능에 크게 영향을 미치지 않는 sub-tree를 잘라내는 방법. 계산 속도가 느리지만, 성능 향상이 유의미하게 나타난다.

Multivariate Distribution Trees

모든 input dimension이 decision node에 사용되는 방식.

f_{m} (x) = w_{m}^{⊤} x + w_{m 0} > 0

기존의 decision tree가, 각 feature에 대해서 test function을 하나 씩 만드는 방식이었다면 multivariate tree는 한번에 여러 input을 사용한다.

이를 위해 QDA등이 사용될 수 있으며, Gaussian Distribution등을 가정해 parameter $w$ 를 추정한다.